이전 포스트 : 스칼라, 벡터, 행렬, 텐서
본 포스트는 Deep-Learning-Book-Series-Introduction 을 기본으로 만들어졌습니다. 완벽히 마스터 한 후에 쓴 글이 아니고, 저 또한 공부하며 쓰는 번역에 가깝기 때문에 서로 질문해가며 이해를 도울 수 있으면 좋겠습니다.
이전 포스트에서 …
- 스칼라는 하나의 숫자를 의미합니다.
- 벡터는 숫자(스칼라)의 배열입니다. \[ \boldsymbol{x} =\begin{bmatrix} x_1 \\ x_2 \\ \cdots \\ x_n \end{bmatrix} \]
- 행렬은 2차원의 배열입니다. \[ \boldsymbol{A}= \begin{bmatrix} A_{1,1} & A_{1,2} & \cdots & A_{1,n} \\ A_{2,1} & A_{2,2} & \cdots & A_{2,n} \\ \cdots & \cdots & \cdots & \cdots \\ A_{m,1} & A_{m,2} & \cdots & A_{m,n} \end{bmatrix} \]
- 텐서는 2차원 이상의 배열입니다.
Dot product(matrix multiplication)
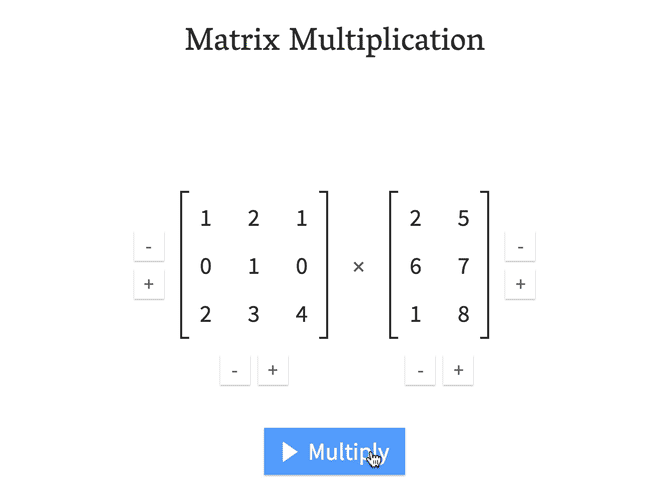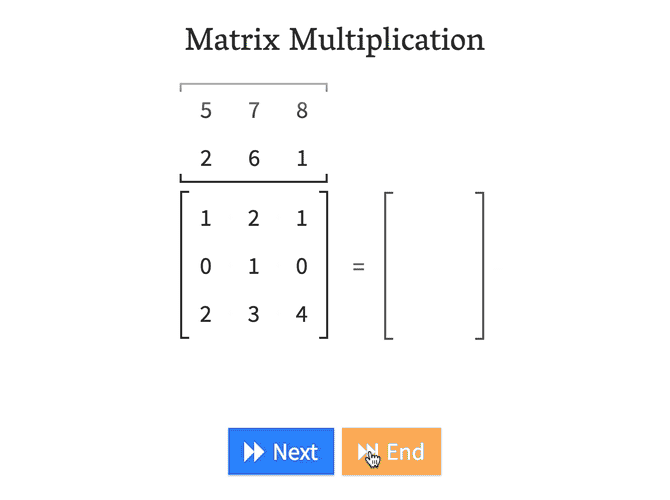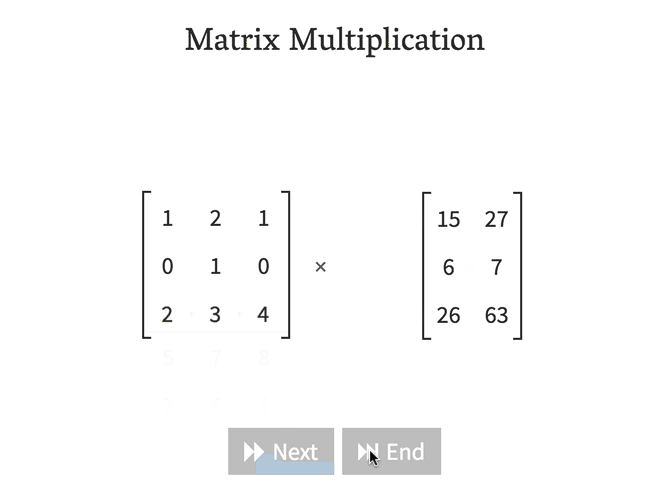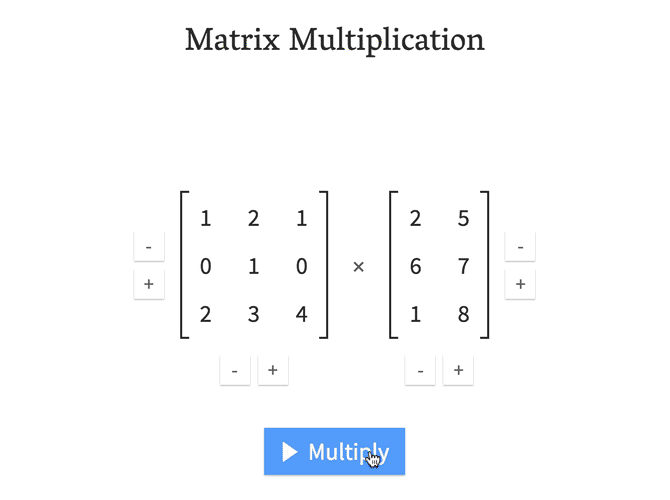
행렬 곱셈의 결과를 모르는 분은 많이 없으시리라 생각됩니다. 다만, 행렬 곱셈의 결과를 어떤 방식으로 도출할 것인지, 행렬 곱셈을 어느 관점에서 바라볼 것인지는 다양한 선택지가 있습니다. 먼저 행렬 곱셈의 정의를 간단하게 적어보겠습니다. \[\boldsymbol{A} : m{\times}n \ matrix\] \[\boldsymbol{B} : n{\times}p \ matrix\] \[\boldsymbol{C} : m{\times}p \ matrix = \boldsymbol{A} \times \boldsymbol{B}, \ when \ \forall i,j \] \[C_{i,j} = \sum\limits_{k=1}^n A_{ik} \cdot B_{kj} = C_{ij}\]
제가 고등학교 때 이해한 행렬 곱셈은 좌측 행렬의 행백터들과 우측 행렬의 열백터들을 곱하면서 한 칸 한 칸 채워나가는 것이었는데요, 단순히 행렬 곱셈의 값을 계산하는 데만 초점이 맞추어진 방법이었습니다. 이후에 나올 선형 시스템을 표현하는 것으로서 행렬을 사용한다면, 더 다양한 관점에서 행렬 곱셈을 바라볼 수 있습니다.
선형 시스템(linear system)
선형 방정식(linear equation)은 우리가 이른 바 연립방정식으로 잘 알고있는 형태입니다. 그 중에서도 1차 연립방정식, 즉 미지수의 차수가 1 이하인 경우를 선형 방정식이라고 합니다. 예를 들어,
\[\begin{cases} y = 2x + 1 \\ y = \frac{7}{2}x +3 \end{cases}\] 위 식은 두 개의 미지수로 이루어진 선형 방정식입니다.
선형방정식의 장점은, 행렬을 통해 선형 시스템 \(\boldsymbol{Ax}=\boldsymbol{b} \)로 표현할 수 있다는 점임니다. 위의 예시는 다음과 같이 표현될 수 있습니다.
\[\begin{cases} 2x-y = -1 \\ \frac{7}{2}x -y = -3 \end{cases}\] \[\begin{bmatrix} 2 & -1 \\ \frac{7}{2} & -1 \end{bmatrix}\cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -1 \\ -3 \end{bmatrix}\]
조금 더 일반화하면 모든 선형 방정식은, \[A_{1,1}x_1 + A_{1,2}x_2 + A_{1,n}x_n = b_1 \\ A_{2,1}x_1 + A_{2,2}x_2 + A_{2,n}x_n = b_2 \\ \cdots \\ A_{m,1}x_1 + A_{m,2}x_2 + A_{m,n}x_n = b_n\] 이 꼴로 변형 될 수 있고(위 예의 x,y가 x1, x2 … 로 일반화 되었습니다.)
아래와 같이 행렬 곱셈으로 표현할 수 있습니다. \[ \begin{bmatrix} A_{1,1} & A_{1,2} & \cdots & A_{1,n} \\ A_{2,1} & A_{2,2} & \cdots & A_{2,n} \\ \vdots & \vdots & \vdots & \vdots \\ A_{m,1} & A_{m,2} & \cdots & A_{m,n} \end{bmatrix} \times \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix} \]
선형 시스템 풀이의 의미
위에서 언급하였듯이, 행렬 곱셈으로 나타낸 선형 시스템을 바라보는 관점은 한 가지만 존재하는 것이 아닙니다. 특히 행렬의 행과, 열 중 어떤 부분을 중심으로 선택하는 가에 따라 여러 가지 의미를 도출해낼 수 있습니다.
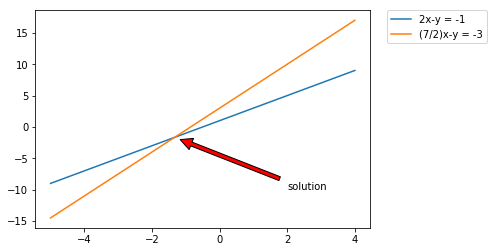
1. 행 기준 관점
\[\begin{bmatrix} 2 & -1 \\ \frac{7}{2} & -1 \end{bmatrix}\cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -1 \\ -3 \end{bmatrix}\] 위의 예를 다시 사용해 봅시다. 이 행렬 곱셈을 행 기준으로 뜯어보면, \[\begin{cases} 2x-y = -1 \\ \frac{7}{2}x -y = -3 \end{cases}\] 와 같은 원래 식들이 튀어나옵니다.
즉 행 기준으로 선형시스템을 바라보면, 여러 조건식들의 교점을 찾는 문제임을 알 수 있습니다.
2. 열 기준 관점
선형 시스템을 열 기준으로 바라볼 수도 있습니다. 이 때 위 식은 다음과 같이 표현됩니다 \[ x \cdot \begin{bmatrix} 2 \\ \frac{7}{2} \end{bmatrix} + y \cdot \begin{bmatrix} -1 \\ -1 \end{bmatrix} = \begin{bmatrix} -1 \\ -3 \end{bmatrix} \] 여기서 숫자로만 이루어진 행렬들을 하나의 벡터로 바라봅시다. 그러면 우리는 우변의 벡터 \(\begin{bmatrix} -1 \\ -3 \end{bmatrix}\)이 좌변의 벡터 \(\begin{bmatrix} 2 \\ \frac{7}{2} \end{bmatrix}\)와 \(\begin{bmatrix} -1 \\ -1 \end{bmatrix}\) 의 선형 결합으로 이루어져 있음을 확인할 수 있고, 그 계수는 각각 스칼라인 \(x\)와 \(y\)입니다.
즉, 열 관점에서 보면 선형 시스템은, 주어진 벡터들에(\(\boldsymbol{A}\)) 특정한 스칼라들(\(\boldsymbol{x}\))을 곱하여 목표 벡터(\(\boldsymbol{b}\))를 만드는 선형결합 과정입니다.
좀 더 일반화 해볼까요? \[ \begin{bmatrix} A_{1,1} & A_{1,2} & \cdots & A_{1,n} \\ A_{2,1} & A_{2,2} & \cdots & A_{2,n} \\ \vdots & \vdots & \vdots & \vdots \\ A_{m,1} & A_{m,2} & \cdots & A_{m,n} \end{bmatrix} \times \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix} \] \(\boldsymbol{A}\)의 i번째 열벡터를 \(\boldsymbol{A}_i\)라고 합시다. 그러면 위의 식은 다음과 같이 표현할 수 있습니다.
\[ x_1 \cdot \begin{bmatrix} A_{1,1} \\ A_{2,1} \\ \cdots \\ A_{m,1} \end{bmatrix} + x_2 \cdot \begin{bmatrix} A_{1,1} \\ A_{2,1} \\ \cdots \\ A_{m,1} \end{bmatrix} \cdots + x_n \cdot \begin{bmatrix} A_{1,n} \\ A_{2,n} \\ \cdots \\ A_{m,n} \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{bmatrix} \] \[ x_1 \cdot \boldsymbol{A}_1 + x_2 \cdot \boldsymbol{A}_2 \cdots + x_n \cdot \boldsymbol{A}_n = \boldsymbol{b} \]
실습
- dot product
import numpy as np
A = np.array([[1, 2], [3, 4], [5, 6]]) # 3x2 행렬입니다
B = np.array([[2], [4]]) # 2x1 행렬입니다
C = np.dot(A, B) # 도트곱은 np.dot 함수를 사용합니다
C # 3x2 행렬에 2x1행렬을 곱했으니 3x1 행렬이 나오리라 예상할 수 있습니다.
array([[10],
[22],
[34]])
다음과 같은 방식으로 구할 수도 있습니다.
C = A.dot(B)
C
array([[10],
[22],
[34]])
도트 곱셈은 결합법칙과 분배법칙이 성립합니다. \[\boldsymbol{A}(\boldsymbol{BC}) = \boldsymbol{AB}(\boldsymbol{C})\] \[\boldsymbol{A}(\boldsymbol{B}+\boldsymbol{C}) = \boldsymbol{AB}+\boldsymbol{AC}\]
A = np.array([[2, 3], [1, 4], [7, 6]]) # 3x2
B = np.array([[5, 3], [2, 2]]) # 2x2
C = np.array([[1,2,3],[4,5,6]]) # 2X3
D1 = (A.dot(B)).dot(C)
D2 = A.dot(B.dot(C))
print(D1)
print(D2)
[[ 64 92 120] [ 57 81 105] [179 259 339]] [[ 64 92 120] [ 57 81 105] [179 259 339]]
A = np.array([[2, 3], [1, 4], [7, 6]]) # 3x2
B = np.array([[5], [2]]) # 2x1
C = np.array([[4], [3]]) # 2x1
D1 = A.dot(B+C)
D2 = A.dot(B) + A.dot(C)
print(D1)
print(D2)
[[33] [29] [93]] [[33] [29] [93]]
하지만 교환법칙은 성립하지 않습니다. \[\boldsymbol{AB} \neq \boldsymbol{BA}\]
A = np.array([[2, 3], [6, 5]]) # 2x2
B = np.array([[5, 3], [2, 2]])# 2x2
AB = np.dot(A, B)
BA = np.dot(B, A)
print(AB)
print(BA)
[[16 12] [40 28]] [[28 30] [16 16]]
그러나, 벡터 간 곱셈에서는 교환법칙이 성립합니다 \[ \boldsymbol{x^{ \text{T}}y} = \boldsymbol{y^{\text{T}}x} \]
x = np.array([[2], [6]]) # 2x1
y = np.array([[5], [2]]) # 2x1
x_ty = x.T.dot(y)
y_tx = y.T.dot(x)
print(x_ty)
print(y_tx)
[[22]] [[22]]
마치며
이번 포스트를 쓰면서 느낀 점은, 역시 선형대수학이 전혀 무엇인지 모르는 분들을 대상으로 작성하기는 쉽지 않을 것 같다는 것입니다.. 아무래도 엄밀하게 설명하기 위해서는 선형성이 무엇인지, 벡터가 어떤 의미를 가지는지 모두 설명해야 하겠지만 저 역시도 완벽하게 이해하고 있는 상황이 아니기 때문에, 어느 정도 배경지식이 있으신 분들에게 복습(이론,코드)을 도와드리는 것을 목표로 잡아야겠습니다.
Reference
- http://twlab.tistory.com/4