이전 포스트 : Linear Algebra
본 포스트는 Deep-Learning-Book-Series-Introduction 을 기본으로 만들어졌습니다. 완벽히 마스터 한 후에 쓴 글이 아니고, 저 또한 공부하며 쓰는 번역에 가깝기 때문에 서로 질문해가며 이해를 도울 수 있으면 좋겠습니다.
정의
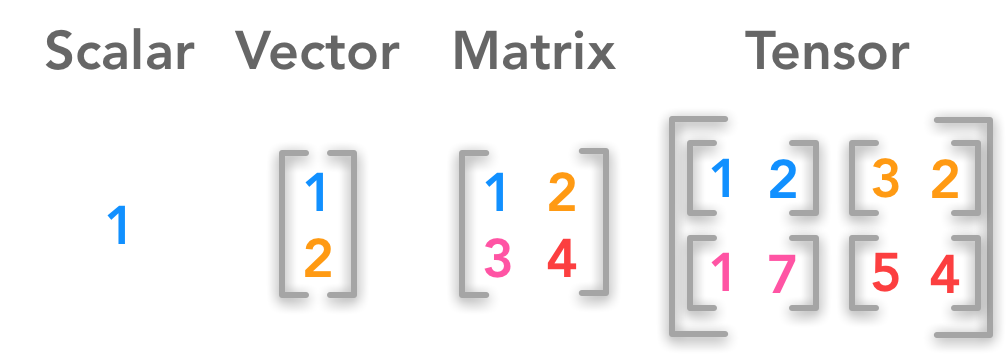
- 스칼라는 하나의 숫자를 의미합니다.
- 벡터는 숫자(스칼라)의 배열입니다. \[ \boldsymbol{x} =\begin{bmatrix} x_1 \\ x_2 \\ \cdots \\ x_n \end{bmatrix} \]
- 행렬은 2차원의 배열입니다. \[ \boldsymbol{A}= \begin{bmatrix} A_{1,1} & A_{1,2} & \cdots & A_{1,n} \\ A_{2,1} & A_{2,2} & \cdots & A_{2,n} \\ \cdots & \cdots & \cdots & \cdots \\ A_{m,1} & A_{m,2} & \cdots & A_{m,n} \end{bmatrix} \]
- 텐서는 2차원 이상의 배열입니다.
기호 표현은 Deep Learning Book에서 채택한대로 사용하겠습니다.
- 스칼라는 소문자의 이탈릭체를 사용합니다. 예시: \(n \)
- 벡터는 소문자의 강조 이탈릭체를 사용합니다. 예시: \(\boldsymbol{x}\)
- 행렬은 대문자의 강조 이탈릭체를 사용합니다. 예시: \(\boldsymbol{X}\)
예제 1. 벡터 표현
np.array를 사용합니다.
import numpy as np # 이 방식의 import를 주로 사용합니다.
x = np.array([1, 2, 3, 4])
x # notebook 기반의 즉시 호출을 사용합니다.
array([1, 2, 3, 4])
예제 2. 3x2행렬 만들기
A = np.array([[1, 2], [3, 4], [5, 6]])
A
array([[1, 2],
[3, 4],
[5, 6]])
형태 확인. shape attribute를 사용합니다.
A.shape
(3,2) # 3x2 행렬
1차원 배열인 벡터는 다음과 같은 shape을 반환합니다.
x.shape
(4, )
벡터는 len 기본 함수를 통해서도 길이를 확인할 수 있습니다.
len(x)
4
전치행렬(Transpose)
기존 행렬 \(\boldsymbol{A}\)에 대해 전치행렬 \(\boldsymbol{A}^T\)는 다음을 만족합니다.
\[ \boldsymbol{A}^T_{i,j} = \boldsymbol{A}_{i,j} \qquad \forall i, j\]
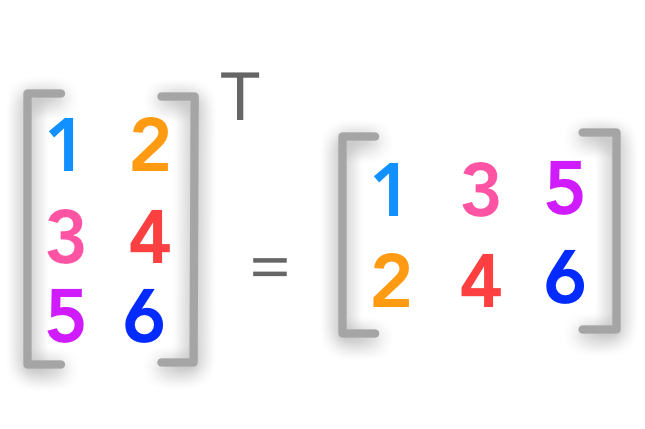
예제 3. 전치행렬 만들기
A = np.array([1,2], [3,4], [5,6]) # 3x2 matrix
A
array([[1, 2],
[3, 4],
[5, 6]])
A_t = A.T # can traspose easily by using attribute T
A_t
array([[1, 3, 5],
[2, 4, 6]])
print(A.shape)
print(A_t.shape)
(3, 2) (2, 3)
기본 행렬 연산(덧셈)
행렬 덧셈은 직관적입니다. \[\boldsymbol{A} + \boldsymbol{B} = \boldsymbol{C} \] \[\iff A_{i,j} + B_{i,j} = C_{i,j} \qquad \forall i, j\] \[\begin{bmatrix} A_{1,1} & A_{1,2} \\ A_{2,1} & A_{2,2} \\ A_{3,1} & A_{3,2} \end{bmatrix}+ \begin{bmatrix} B_{1,1} & B_{1,2} \\ B_{2,1} & B_{2,2} \\ B_{3,1} & B_{3,2} \end{bmatrix}= \begin{bmatrix} A_{1,1} + B_{1,1} & A_{1,2} + B_{1,2} \\ A_{2,1} + B_{2,1} & A_{2,2} + B_{2,2} \\ A_{3,1} + B_{3,1} & A_{3,2} + B_{3,2} \end{bmatrix}\]
예제 4. 행렬 덧셈 해보기
A = np.array([[1, 2], [3, 4], [5, 6]])
B = np.array([[2, 5], [7, 4], [4, 3]])
print(A)
print(B)
[[1 2] [3 4] [5 6]] [[2 5] [7 4] [4 3]]
# Add matrices A and B
C = A + B
C
array([[ 3, 7],
[10, 8],
[ 9, 9]])
예제 5. 행렬에 스칼라 더해보기
행렬과 스칼라의 덧셈은, 모든 원소에 스칼라를 더하는 것과 같습니다
A = np.array([[1, 2], [3, 4], [5, 6]])
B = np.array([[2, 5], [7, 4], [4, 3]])
print(A)
print(B)
array([[ 5, 6],
[ 7, 8],
[ 9, 10]])
예제 6. NumPy에서, 다른 크기의 행렬 간의 덧셈
A = np.array([[1, 2], [3, 4], [5, 6]]) # 3x2
B = np.array([[2], [4], [6]]) # 3x1
print(A)
print(B)
[[1 2] [3 4] [5 6]] [[2] [4] [6]]
이렇게 크기가 다른 행렬 간의 덧셈을 Broadcasting이라고 합니다. 크기가 작은 B가 더 큰 A에 맞추어 한 열 더 복제되어 더해집니다.
# Broadcasting
C = A + B
C
array([[ 3, 4],
[ 7, 8],
[11, 12]])
마치며
아무래도 첫 부분이라 정의가 많습니다. 다음 장부터는 설명할(배울) 거리가 많았으면 좋겠습니다…